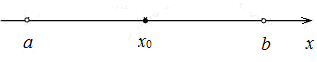
Определение 1.9.1. Окрестностью точки x ₀ называется любой интервал, содержащий точку x ₀ :

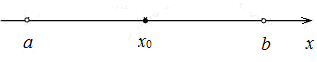
Рис. 8

x∈(α;b).

Определение 1.9.2. δ-окрестностью точки x ₀ называется интервал (x ₀ -δ; x ₀ +δ), длина которого 2δ, симметричный относительно x ₀ :

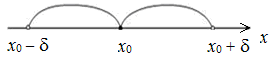
Рис. 9

x∈(x ₀ -δ;x ₀ +δ)⇒|x-x ₀ |<δ.

Определение 1.9.3. Проколотой δ-окрестностью точки x ₀ называется δ-окрестность точки x ₀ без самой точки x ₀ :

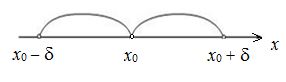
Рис. 10

x∈(x ₀ -δ; x ₀ )∪(x ₀ ; x ₀ +δ)⇒0<|x-x ₀ |<δ.

Определение 1.9.4. Число А называется пределом функции f ( x ) при x → x ₀ , если для любого малого числа ε > 0 существует такое малое число δ=δ(ε)>0, что для любого x , принадлежащего D( f ) и проколотой δ-окрестности точки x ₀ , т.е. 0<|x-x ₀ |<δ, выполняется неравенство: |f(x)-Α|<ε.

Итак: 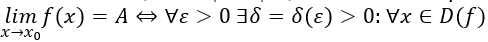и

0<|x-x ₀ |<δ⇒|f(x)-Α|<ε.