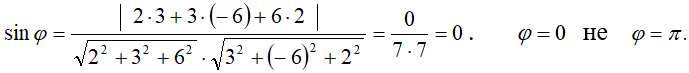Кеңістікте түзу мен жазықтықтың өзара орналасуының үш жағдайы болуы мүмкін:  Түзу мен жазықтық бір нүктеде қиылысады; түзу мен жазықтық  параллель; түзу  жазықтықта жатады.

Айталық, π - жазықтық жалпы теңдеумен : Ax + By + Cz + D = 0, ал L  түзуі канондық теңдеумен: (x - x 0 )/l = (y - y 0 )/m = (z - z 0 )/n  берілген делік.  Түзудің теңдеуінен оның бойындағы M 0 (x 0 ; у 0 ; z 0 ) нүктені  және оның бағыттаушы векторын s = {l; m; n} білеміз. Ал жазықтықтың теңдеуінен нормаль векторды n = {A; B; C} көреміз.

  1. Егер түзу мен жазыққтық қиылысса, онда түзудің бағыттаушы векторы жазықтыққа параллель емес, яғни нормаль вектор мен бағыттаушы векторлар перпендикуляр емес, олардың скаляр көбейтіндісі нольге тең болмайды. Бұл теңсіздік коэффициенттер арқылы осылай жазылады:
    2. A1 + Bm + Cn ≠ 0. (1)
  2. Егер түзу жазықтыққа параллель болса немесе түзу жазықтыққа тиісті болса, онда мына шарт орындалады: s ⊥ n, яғни
    3. A1 + Bm + Cn = 0. (2)
  3. Және түзу жазықтыққа тиісті болғанда M 0 (x 0 ; у 0 ; z 0 ) нүктесі жазықтыққа тиісті, яғни (2) шартпен қоса
    Ax 0 + Bу 0 + Cz 0 + D = 0 (3)
    шарты орындалады.

Сонымен түзу мен жазқтықтың орналасу жағдайларын анықтау үшін келесі шарттарды тексереміз:

Егер L түзуі жалпы теңдеумен

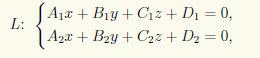
берілсе, онда түзу мен жазықтықтың орналасуын нақтылау үшін келесі әдіспен жүреміз: түзудің теңдеуі мен жазықтықтың теңдеуінен үш белгісізді үш теңдеудің сызықтық жүйесін құрамыз.

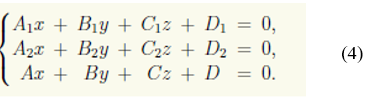
Егер бұл жүйенің шешімі болмаса, онда түзу мен жазықтық параллель. Егер бұл жүйенің бір ғана шешімі болса, онда түзу мен жазықтық қиылысады. Яғни (4) жүйенің анықтауы

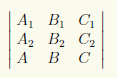
нольден өзгеше болады.

Егер (4) жүйенің шексіз көп шешімі болса, онда түзу жазықтықта жатады.

Түзу мен жазықтықтың арасындағы бұрыш. Түзу L: (x - x 0 )/l = (y - y 0 )/m = (z - z 0 )/n мен жазықтық π: Ax + By + Cz + D = 0 арасындағы бұрыш 0° пен 90° арасында өзгере алады. Бұл бұрыштың синусы |cosψ|-ге тең, мұндағы ψ — бұрышы бағыттаушы s вектор мен n нормаль вектор арасындағы бұрыш.

бұдан

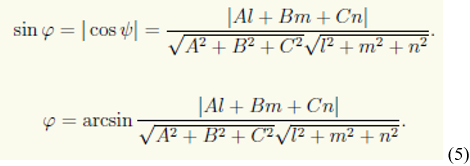
Түзу мен жазықтықтың перпендикулярлық шарты. Бағыттаушы вектор мен нормаль вектордың коллинеарлығынан:

A/l = B/m = C/n. (6)

Мысал: (x + 3)/2=(y - 3)/2 = z/6 ( l ) түзуімен 3x - 6y +2z +8 = 0 ( Q )жазықтығы арасындағы бұрышты есептеу керек.

Шешуі. 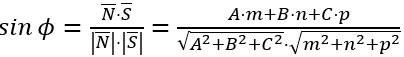формуласы бойынша