ҚАРЖЫЛЫҚ МЕНЕДЖМЕНТ

Пайыздық мөлшерлеме. Ақшалық ағын. Аннуитеттер. Инфляция қалпын ескеру





Пайыздық мөлшерлеме. Қарапайымды пайыздық өсім мөлшерлемесі дегеніміз өсім есептелетін базалық соманың әрқашан да тұрақты көлемде болатын мөлшерлемесі.

Мұнда несиелік барлық мерзім бойы есептелетін П пайыздар мына формула бойынша шығарылады:


П = А · м · қ, (2)


бұл арада м - жылмен саналатын несие мерзімі, қ - қ арапайымды пайыздық өсім мөлшерлемесі.


Пайыз көлемін шығаратын өлшемді (2) оның қатынасын анықтайтын есепке (1) енгізіп, қарапайымды пайызбен шығарылатын өсім сомасының (Ө) формуласын табамыз:


Ө = П · (1 + м · қ). (3)


Мұндағы (1 + м · қ) = к көбейткіші қарапайымды пайыздар өсімі көбейткіші деп аталынады.

Несиенің мерзімі мына формуламен шығарылады:



мұнда с – несие уақытының күн саны, Ж – жылдың барлық күн саны.


Қолданылатын әдістеме бойынша жыл мерзімі екі жолмен есептелінеді: жәй пайыздар – Ж – 360-қа; дәлме-дәл пайыздар – Ж – 365 (366)-ке тең болады.

Күрделі пайыздық өсім мөлшерлемесі дегеніміз өсім есептелетін базалық соманың өзгермелі көлемде болатын мөлшерлемесі, яғни пайыздар пайыздарға шағылады.


Ө = А(1 + қ).


Дисконтталған жағдайда алдағы төлемнің қазіргі құны алынып тасталынады. Басқаша айтқанда, алдағы Ө төленімінің м мерзімі өткеннен кейін қ дисконттік мөлшерлемемен берілетін қазіргі А көлемі анықталынады.

Қарапайымды пайыздар үшін:

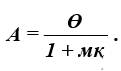
Күрделі пайыздар үшін:

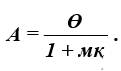
Көбейткіштер 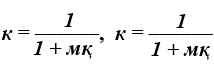− дисконттық көбейткіштер деп аталынады.

Айырмашылық Ө - А дегеніміз Ө өсім сомасынан түсетін дисконтті білдіреді.

Есептік мөлшерлеме дегеніміз вексельдер есебі жүргізілгенде қолданылатын мөлшерлеме.

Баламалы пайыздық мөлшерлеме деп бірін-бірі ауыстырып пайдаланылғанда қаржылық бір нәтиже беретін кезкелген екі мөлшерлемені айтамыз, яғни қаржылық іс-әрекет барысында екі жақтың да арақатынасы өзгермейді деген сөз.

Енді қарапайымды және күрделі өсім мөлшерлемелері бойынша араларындағы қатынастарының баламалылығын анықтайық. Бұл арада қаралатын мөлшерлемелердің пайдаланғанда алғашқы және өскен сомалар бірдей болады деп қараймыз. Сондықтан қойылған есепті шешу үшін өсімдер өбейткіштерін біріне бірін теңестіреміз. Сонда барып біз мынаны табамыз:


1 + мқ = (1 + ү) ,


бұл арада қ – қарапайымды пайыздық мөлшерлеме, ү – күрделі пайыздық мөлшерлеме, м – жылмен саналатын несие мерзімі.

Осы теңдеуді ү және қ қатысты шығаратын болсақ, сәйкес мыналарды табамыз:

өсімнің күрделі пайыздық мөлшерлемесін –

өсімнің қарапайымды пайыздық мөлшерлемесін –

Ақшалық ағын. Аннуитеттер. Төленімдер ағындары – ол уақыт барысында дәйекті түрде өтетін төленімдер (облигация купондарын, пенсия және т.с.с. төлеулер).

Аннуитеттер (қаржылық рента) дегеніміз тек бір бағытта ғана атқарылатын және де аралары бірдей болып келетін төлемдер, яғни тұрақты жүйелі түсімдер.

Тұрақты емес ағындар – бір бөлігі оң шама (түсім), қалғаны – теріс шама (басқа ұйымдарға төлеулер) болып келетін төленімдер. Төленімдер ара уақыты бұндай жағдайда біркелкі болмауы да мүмкін.

Төленім ағынының өсірілген сомасы – мерзім соңында күрделі пайыздық мөлшерлемелер қосылған барлық төленімдер сомасы.

Төленімдер ағынынң қазіргі құны – күрделі пайыздық мөлшерлеме бойынша мерзім басында дисконтталған барлық төленімдер сомасы.

Мысалға, ішінде:

Т – оң (+ белгідегі) немесе теріс (- белгідегі) түрлі төленімдер;

у1, 2… – с = 1 + 2 + … + С нөмірлері бойынша жасалынған төленімдер уақыты;

С – төленімдер саны;

к – жылына бір рет есептелетін өсірілген соманың күрделі пайыздық мөлшерлемесі;

ус – төленімдердің жалпы мерзімі көрсетілген мәліметтерды алатын болсақ, төленімдер ағынының жалпы жағдайы сызба түрінде мынадай болмақ:



Осындай төленімдер ағынының өсірілген сомасы оның анықтамасы бойынша мына формуламен есептелініп шағарылады:



Төленімдер ағынының қазіргі құны Қ мына формуламен есептелініп шағарылады:



Жылдық тұрақты рента деп, жыл бойы өзгермейтін рентаны айтамыз.


Келісілген мерзімнің басында және аяғында сай келер төленімдер кезеңіне байланысты түскен пайдалар әр түрлі: мерзім соңында атқарылатын төленімдер – постнумерандо (қарапайымды) пайда деп; мерзім басында атқарылатын төленімде – пренумерандо пайда деп; мерзім ортасында атқарылатын пайда деп,
аталынады.

Төленімдер жыл бойы б – бірнеше сан рет атқарылса, онда пайда б-мерзімді, немесе жылына бірнеше рет төленгенде түсетін пайда деп аталынады.

Инфляция қалпын ескеру. Инфляция қалпы есепке алынбай жасалынған ақшалық ағындардың ақырғы қорытындысы шамамен ғана шыққан болып қалады. Инфляция үрдүстеріне байланысты түрлі түсініктер бар.

Соманың нақтылы нарқы (Н) – инфляция барысында құнсызданғаннан қалған сома мынадай формуламен есептелінеді:



бұл арада Иб – баға индексі, немесе белгілі бір тауар топтамасына қатысты оның өсу қарқыны.

Баға индексі зерделеніп отырған мерзімдегі бағаны базалық мерзімдегі бағаға шағып, сол қатынасты пайызбен шығарып анықтайды.

Инфляцияның өсу қарқыны (Қ) дегеніміз белгілі бір мерзім арасындағы баға өсімінің салыстырмалы көрсеткіші:


Қ = Иб – 1.


Инфляция барысында ақшаның құнсыздануы инфляциялық сыйлық есебіндегі қосымша табыс беретін мөлшермен өтелінеді. Ең ақырғы мөлшерлемені брутто-мөлшерлеме деп атайды.